01背包算法 | ACM

　　0_1背包，背包算法中最基础的算法之一，我已知的其解题方法有两种：1、动态规划（DP）。2、DFS+剪枝。本文讲的是01背包的动态规划解法。

0-1背包问题：

　　给定 n 种物品和一个容量为 C 的背包，物品 i 的重量是 Wi ，其价值为 Vi 。
　　问：应当如何选择装入背包的物品，使得装入背包的物品的总价值最大？
　　假设一个函数B是求解总价值的函数，有三个变量，n、C与x；其中x代表着每一种物品的状态，拿/不拿；
　　所以我们的优化目标就变为

　　其展开公式为

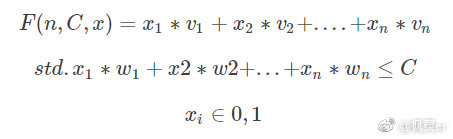
　　x的取值范围为0或1，代表着这个物品我们可以选择拿或者不拿，我们需要找出一个这样的01组合，使F(n,C,x) 最大。
　　那么有这样一个状态方程：

　　当成二维数组来看：B i 代表当【放到第 i 个物品时，此时的容量还剩 j 】这个时候的价值。我们可以选择第 i 个物品放或不放。
　　如果不放的话：B i =B i-1 ；就相当于放了前 i-1 个物品中的物品，注意：不一定是前 i-1个物品全放进了背包（描述不清楚，反正就那么个状态，相当于 i-1 时的状态完全不变转移到 i 中）
　　如果第 i 个物品放进去的话 F i =F i-1 + vi；因为第 i 个物品放进去了，所以在前面 i-1 状态的基础上，容量减去 Wi，价值加上 Vi（前提是 Wi < j 时）；
　　但是有些人（比如我）会挺纳闷，在放得下的前提下从（F i-1 ,F i-1 ] + vi[ i ] ） 这两个中选择最大的，那肯定是加入了第 i 个物品的大呀，这还需要思考吗？请看下图：

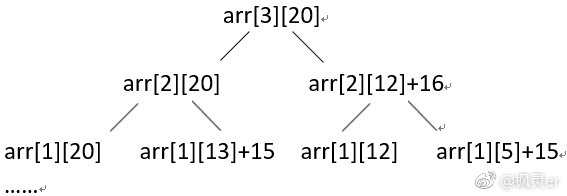
　　假设有3个物品，重量分别为：9、7、8；价值分别是：10、15、16，背包容量是20.
　　其实只要我们按照那个公式套进去，就会发现，每个物品放与不放的情况都会被遍历到，
　　但是回到上面的问题，F i-1 < F i-1 + vi 是不错，但是你放了第 i 个物品，也许你放了第 i 个物品，放不下 i+1 个物品了，但是 vi > vi
　　所以每种情况我们都要遍历过，选出最优的。

　　其实还有一种对这个问题的解释，不过我没看懂，但是我还是把它放上来：
　　>F i-1 < F i-1 + vi 是不错，但是你放了第 i 个物品，假设是这个例子的最后一个物品，前面你或许就得少放一个物品了。

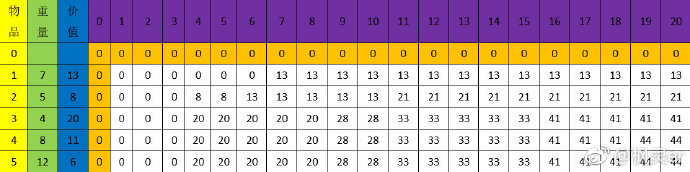
　　大家请看上图，思路就是从左上角开始，一行一行的求出所有放与不放的可能，右下角的44就是我们要求的答案了；但是需要注意的是，
其实很多数据我们根本用不着，从最后一行往上数，我们要的数据个数只是1、2、4、8、16个而已。

示例代码

#include<stdio.h>
#include<math.h>

void zeroOne(int *arr);

int main()
{
    int m,n; //m,n分别表示背包能装重量和物品个数
    scanf("%d %d",&n,&m);
    
    //-----------------------------------//
    
    int *w,*v;//建立两个个w与v一一对应的数组，其实我觉得用结构体会更好一点吧？
    w = (int *)malloc(sizeof(int *)*n);
    v = (int *)malloc(sizeof(int *)*n);
    
    int **arr;//动态分配二维数组
    arr = (int **)malloc(sizeof(int *)*(n+1));
    for(int i = 0;i <= n;i++)
    {
         arr[i]=(int *)malloc(sizeof(int)*(m+1));
    }
    
    //-----------------------------------//
    
    int j;//输入数据
    for(i=0;i<=n-1;i++)
        scanf("%d%d",&w[i],&v[i]);
    
    zeroOne(arr);
    
    printf("%d",arr[n][m]);
    free(arr);
    free(w);
    free(v);
    return 0;
}

void zeroOne(int *arr)
{
    for(i=0;i<=n;i++)
         for(j=0;j<=m;j++)
         {
             if(i==0 || j==0)    //0容量或者0物品置0
                 arr[i][j]=0;
             else if(w[i-1]<=j)
                 arr[i][j]=max(arr[i-1][j],arr[i-1][j-w[i-1]]+v[i-1]);
             else
                 arr[i][j]=arr[i-1][j];
         }
}

　　在这里我有一个问题，在我用//--//框住的区间内，动态分配数组和直接定义数组有什么区别，动态分配有什么优点吗？

例题示范

　　在这里我想用hdu的一道题饭卡作为例题，具体代码在下边：

#include<stdio.h>
#include<math.h>

int max(int a,int b);
void px(int *a);

int main()
{
    int card,n;
    while(~scanf("%d",&n),n)
    {
    int dishes[1012] = {0};
    int zeroOne[1012] = {0};
        for(int i = 0;i < n;i++)
        {
            scanf("%d",&dishes[i]);
        }
        scanf("%d",&card);
        if(card < 5)
        {
            printf("%d\n",card);
            continue;
        }
        card -= 5;
        px(dishes);
                            //数据接收
        
      for(int i = 0; i < n-1 ;i++)
        {
//            printf("%d",i);
            if(dishes[i] == 0)
                break;
            for(int j = card;j >= dishes[i];j--)
            {
                zeroOne[j] = max(zeroOne[j],zeroOne[j-dishes[i]]+dishes[i]);
            }
        }

//      for(int i = 0;i < 50;i++)
//        {
            printf("%d\n",(card+5-zeroOne[card]-dishes[n-1]));
//        }

  
    }

    return 0;
}

void px(int *a)
{
    int i,j;
    int temp;
    for(i = 0;i < 1012;i++)
    {
        if(a[i]==0)
            continue;
        temp = a[i];
        j = i-1;
        while(j>=0&&a[j] > temp)
        {
//            printf("j = %d\n",j);
            a[j+1] = a[j];
            j--;
        }
        a[j+1] = temp;
//        printf("i = %d\tj = %d\ttemp = %d\n\n",i,j,temp);
    }
}

int max(int a,int b)
{
    if(a > b)
        return a;
    else
        return b;
}

参考文章：01背包(详解)-剑冢