浮点数的标准 —— IEEE Floating Point(IEEE754)
- 此标准在1985年建立
- 浮点数的二进制表示与整数相似,每一位的二进制位数乘上那一位的二进制权重,求和之后就是二进制数的十进制表示,本质上是没有区别的。不过小数点之后的权重都是小于0的。如图:
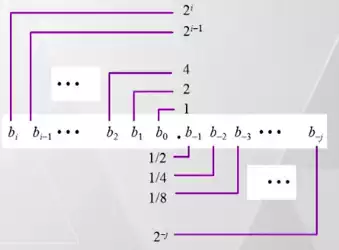
- 用数学公式表达就是:$ \sum\limits_{k=-j}^i b_k · 2^k $
浮点数示例:
- 根据上图的小数部分的分数表示,我们可以得到以下表:
| 值 | 二进制表示 |
|---|---|
| 5.(3/4) | 101.11 |
| 2.(7/8) | 10.111 |
| 0.(63/64) | 0.111111 |
局限性:
- 只能精确地表示 X/$2^k$ 这样的数据。
| 值 | 二进制表示 |
|---|---|
| 1/3 | 0.01010101[01]... |
| 1/5 | 0.00110011[0011]... |
| 1/10 | 0.000110011[0011]... |
计算机中的浮点数表示:
数字表示:
$(-1)^s M 2^E$
- 符号位:s
- 尾数:M 一个位于[1.0 ,2.0) 的一个小数。
- 阶码:E 表示2的E次幂
- 阶码

- exp域:E
- farc域:M
- 单精度浮点数:exp域宽度8 bits,farc域宽23bits,共32bits。
- 双精度浮点数:exp域宽度11 bits,farc域宽52bits,共64bits。
- 扩展精度浮点数:exp域宽度15 bits,farc域宽63bits,共80bits。(1 bit wasted)【很少见,不做要求】
浮点数的类型:
规格化浮点数
满足条件:
- exp ≠ 000...0 且 exp ≠ 111...1
真实的阶码值E需要减去一个偏置(biased)量
E = Exp - Bias
- Exp:exp域所表示的无符号数值
Bias的取值:
$2^(e-1) - 1$
- 单精度数:127 (Exp:1...254,E: -126...127)
双精度数:1023 ( Exp:1...2046,E: -1022...1023)
- farc域的第一位隐含为1
M = 1.xxx...$x_2$
- 因此,第一位的“1”可以省略
000...0:M = 1.0
1111...1:M = 2.0 - \boldsymbol{\epsilon}
- 示例:
Float F = 15213.0
- $15213$ = $11101101101101_2$ = $1.1101101101101_2$ X $2^1$$ 3$
- 尾数
M = $1.1101101101101_2$
farc = $11011011011010000000000_2$
阶码:
E = 13
Bias = 127
Exp = 140 = $10001100_2$
结果如下图:

非规格化浮点数(Denormalized)
满足条件:
exp = 000...0
其他域的取值:
E = -Bias + 1
M = 0.xxx...$x_2$
具体示例:
exp = 000...0 ,farc = 000...0
表示0
注意有+0和-0的区别
exp = 000...0 ,farc ≠ 000...0
表示非常接近0的浮点数
会逐步丧失精度(Gradual underflow)
一些特殊值
- 满足条件:
exp = 111...1 具体示例
exp = 111...1,frac = 000...0
- 表示无穷
可用于表示数值的溢出 - 有正无穷和负无穷
- 表示无穷
- 满足条件:
exp = 111...1,frac ≠ 000...0
- not-a-number(NaN)